한줄요약
드로우 콜은 같은 리소스와 같은 레이어 ID라는 두 가지 조건이 동시에 만족되어야 하나로 합칠 수 있습니다.
UMG에서의 드로우 콜
언리얼 공식 문서에는 드로우 콜과 관련하여 이런 설명이 있습니다:
같은 텍스처 아틀라스에 들어있는 스프라이트는, 렌더링할 때 같은 레이어를 공유하는 경우 슬레이트에 일괄 배치시킬 수 있습니다. 즉 드로 콜 수 예산이 빠듯한 플랫폼에서는 Paper2D 스프라이트를 브러시 입력으로 사용하는 경우 UMG 와 슬레이트 위젯의 렌더링 효율이 크게 향상된다는 뜻입니다.
약간의 비약을 섞어 정리해보면 이렇게 이해할 수도 있습니다.
- 같은 레이어에 같은 리소스를 사용하면 드로우 콜이 줄어든다
- Sprite를 사용한다면 Sprite Atlas를 사용하여 다양한 이미지들의 드로우 콜을 줄일 수 있다
UMG에 나타나는 항목을 크게 Text, Texture, Sprite, Material 요정도로 볼 수 있는데 1번은 모든 UI항목에 적용되지만 2번은 Sprite만 해당됩니다.
드로우 콜 실험들
UMG의 드로우 콜 수 확인은 게임내 콘솔 창에서 Stat Slate 명령으로 볼 수 있습니다. 에디터에서 직접 키는 경우(PIE) 에디터 자체의 드로우 콜 수도 더해지기 때문에 독립형 게임으로 띄운 상태에서 보는 것이 좋습니다.
아래 그림에서 빨간색 숫자는 레이어 ID를 의미합니다.


3개의 텍스트 블록입니다. 동일한 폰트를 사용하기 때문에 드로우 콜은 1입니다. 폰트가 다르면 드로우 콜이 분리됩니다. 또한 Vertical Box는 자식들에게 같은 레이어 ID를 부여하기 때문에 드로우 콜을 관리하는 데 유용합니다.


3개의 이미지가 있습니다. 셋 모두 다른 텍스쳐이기 때문에 드로우 콜은 3입니다.


셋 모두 같은 이미지입니다. Sprite가 아닌 텍스쳐를 사용했기 때문에 드로우 콜이 3으로 나올 것으로 예상했지만 같은 Vertical Box 안에 있기 때문에 드로우 콜이 1로 나옵니다. 같은 리소스이기 때문에 알아서 최적화를 해 준 것으로 보입니다.
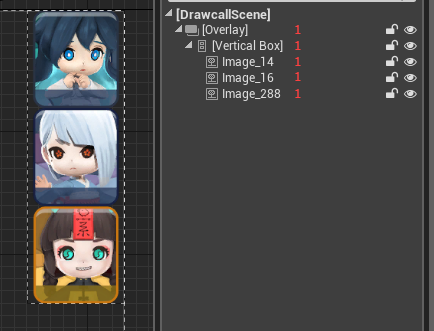

이미지가 서로 다르지만 같은 Atlas를 공유하는 Sprite로 설정했습니다. 드로우 콜은 1입니다.
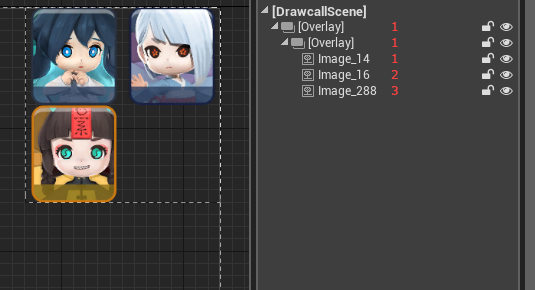

같은 아틀라스를 쓰는 Sprite이지만 Vertical Box 대신 Overlay로만 바꿨을 뿐인데 드로우 콜이 3이 되었습니다. Overlay는 모든 자식들에게 레이어 ID를 1씩 증가시키면서 부여하기 때문에 모든 드로우 콜이 분리됩니다.


다시 Vertical Box로 돌리고 이번에는 각 이미지를 Overlay로 감싸보았습니다. 놀랍게도(?) 드로우 콜이 1로 나옵니다. Vertical Box 아래 오버레이들은 같은 레이어 ID를 가지고 있고 오버레이의 첫번째 자식도 오버레이와 같은 레이어 ID를 가지게 되기 때문에 결국 모든 Sprite의 레이어 ID가 같아지고 결국 드로우 콜이 1로 나왔습니다.


Vertical Box 아래 Horizontal Box를 추가해서 이미지들의 hierarchy가 달라지게 했습니다. hierarchy만 보면 드로우 콜이 나뉘어야 할 것 같지만 여전히 드로우 콜은 1입니다. Vertical Box나 Horizontal Box는 레이어 ID를 바꾸지 않기 때문입니다.
레이어에 영향을 미치는 컨테이너
레이어 ID를 유지하거나 분리시키는 기준은 각 위젯의 구현별로 다 다르기 때문에 하나하나 살펴보고 정리해 두는 것이 좋습니다. 직접 알아보려면 각 UMG 위젯별로 연관된 Slate 위젯 클래스를 찾은 뒤 그 클래스의 OnPaint() 함수에서 레이어 값을 어떻게 처리하고 리턴하는지 확인해 보면 알 수 있습니다.
자주 쓰이는 것들 몇 가지를 정리해 봤습니다.
레이어 ID를 유지하는 위젯들
VerticalBoxHorizontalBoxSizeBoxScaleBoxUniformGridPanelWrapBox
레이어 ID를 증가시키는 위젯들
Overlay: 첫 번째 자식 위젯은 레이어 ID가 증가되지 않습니다.Border
상황에 따라 다른 위젯들
GridPanel: 슬롯마다 레이어를 직접 지정하는 게 가능합니다. 자식들을 순차적으로 돌면서 레이어가 달라질 때마다 새로운 레이어 ID를 부여하는 식입니다.ScrollBox: 박스 자체는 레이어 ID가 유지되지만 스크롤바는 레이어 ID가 1 증가합니다.Canvas: 프로젝트 세팅 창에서 *엔진 - 슬레이트 세팅*에서bExplicitCanvasChildZOrder변수를 켜 주면 직접 지정한 슬롯의 ZOrder 값을 기준으로 Layer ID를 부여합니다. Canvas 자체의 레이어 ID를 사용하지 않지만 ZOrder 값으로 자식들의 레이어 ID를 통일시키는 것이 가능하다.
bExplicitCanvasChildZOrder를 설정하지 않으면 Overlay와 거의 동일하게 동작합니다.
어떻게 위젯 디자인을 해야 할까?
드로우 콜을 최대한 줄이는 위젯 디자인을 하려면 아래 팁이 도움이 될 수 있습니다.
- 최대한 레이어 ID를 유지하는 위젯 위주로 만들어 봅니다.
- Overlay 위젯은 자식을 하나만 가지도록 한다. 여러개의 자식을 가지는 경우 절대 드로우 콜이 합쳐지지 않습니다!
- Canvas 위젯은 슬롯의 ZOrder 값을 점검해 봅시다. 같은 값이면 드로우 콜을 줄일 기회가 되지만 겹치게 되는 경우 z-fighting이 생길 수 있습니다.
- Sprite Atlas Group을 사용합니다. Sprite Atlas Group은 여러 Sprite들을 큰 텍스쳐 몇 개로 합쳐 드로우 콜 수를 획기적으로 줄이는 데 도움이 됩니다.
(2017년에 작성했던 글을 정리하여 업로드했습니다)
'Programming > Unreal Engine' 카테고리의 다른 글
| (인증의 늪) 언리얼 Online Services + Steam + EOS 인증 = ??? (1) | 2026.01.08 |
|---|---|
| 팰월드 모드 분석 (feat. 언리얼) (0) | 2024.02.08 |
| [UE4] 2D 게임용 콘솔 변수 설정하기 (0) | 2021.12.29 |
| 안드로이드 ndk 디버그하기 with gdb (0) | 2019.02.23 |
| 언리얼 애셋 의존성 관리 (0) | 2017.08.01 |
